Taylor series on sin
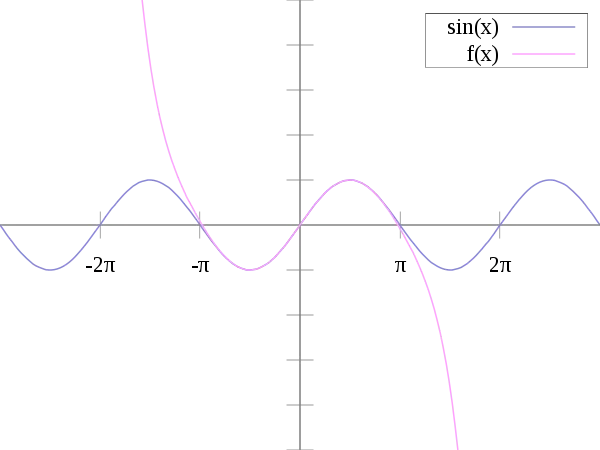
The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full period centered at the origin.
This library uses degree 7 Taylor polynomials for sin as default source = Wikipedia
If you want to do this in your own system, please look at the installation part of our documentation. I know literally 1984
If you have completed the installation, you will get something like this in your directory.
.
├── CMakeLists.txt
├── demo.c
├── LICENCE.txt
├── modules
│ ├── allocators.c
│ ├── allocators.h
│ ├── common_bindings.h
│ ├── errors_and_logging.c
│ ├── errors_and_logging.h
│ ├── literal_array.c
│ ├── literal_array.h
│ ├── math.c
│ └── math.h
└── README.mdThis might seem scary at first. Because it is. This library uses Cmake to build itself, but you can use whatever build system you want.
Just make sure to know that the accuracy of the math.h/c module will be based on your compile flags (ie. --ffast-math, -Ofast ).
Our Trigonometry functions and exponential functions rely on them, and here is the full list of them.
// exponential functions; //
long double sml_exp_pi(void); // Returns the exponential value of x (e^pi).
long double sml_exp(double x); // Returns the exponential value of x (e^x).
long double sml_log2(double x); // Returns the base 2 logarithm of x.
long double sml_log10(double x); // Returns the base 10 logarithm of x. But wit high accuracy
long double sml_log_e(double x); // Returns the natural logarithm of x (base e). But wit high accuracy
long double sml_log_pi(double x); // Returns the natural logarithm of x (base pi). But wit high accuracy
long double sml_nlog(double x, double n); // Returns the natural logarithm of x (x^n). But wit high accuracy
// power functions that are not bound to whole numbers; //
long double sml_pow(long double base, long double expo); // Returns x raised to the power of y (x^y).
double sml_sqrt(double n); // Returns the square root of x.
double sml_nth_root_double(double x, sml_size_t_s n); // Returns the nth root of xAnd it will affect your trigonometric functions as well. Since we cannot use the built-in __sin(x), __cos(x) or __tan(x) the algorithm used
is the Taylor series. If you are a mortal computer programmer like me here are some gifs to explain it
Taylor series on sin

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full period centered at the origin.
This library uses degree 7 Taylor polynomials for sin as default source = Wikipedia
Taylor series on
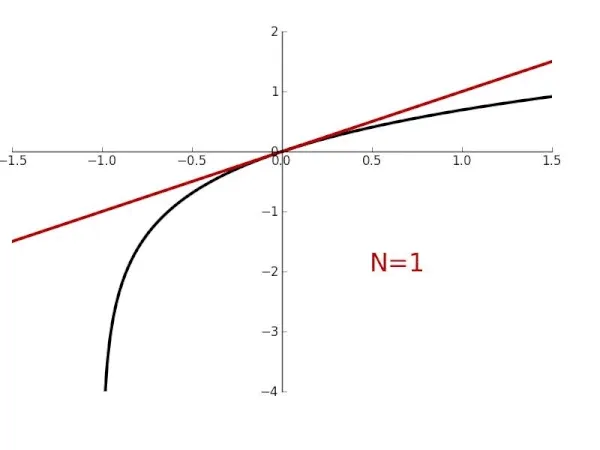
The Taylor approximations for (black). For x > 1, the approximations diverge.
As you can see Taylor polynomials are not the best at approximation in higher values of but it’s good enough
source = Wikipedia
So let’s put this newly learned information to use. Let’s make a quick script for testing this library accuracy.
the code is
#include <stdio.h>
#include "modules/errors_and_logging.h"
#include "modules/common_bindings.h"
#include "modules/math.h"
int main(void) {
printf("hello you!\n");
printf("this is a file where you can try sml_lib without copying it :D\n");
sml_error_config err_conf = init_sml_error(
"SML_SANDBOX",
false,
NULL
);
// math.h does not rely on any preexisting math library. Let's it's check accuracy!
printf("%f", LOGARITHM_ACC);
// since we know that sin^2 + cos^2 = 1
for (sml_size_t degree = 0; degree < 90; degree++) {
printf("sin = %f, cos = %f, Accuracy = %f\n", sml_sin(degree), sml_cos(degree),
sml_float_abs((sml_pow(sml_sin(degree), 2) + sml_pow(sml_cos(degree), 2))));
}
// note that using --ffast-math will change the output.
// this is not because of any fancy tricks. This is just a pure math/skill issue.
sml_throw_error(&err_conf, ERROR_OK, LOG_SEVERITY_INFO, "DONE!, %s", "With Style");
return 0;If your system is fully and correctly set up your margin of error should be ~0.1.
If not you might wanna tweak the settings on the math.h file and if the issue persists please open an issue on the
git repository. Happy coding.